1.4 无源带通滤波器

在前面的教程中，我们已经学习了低通滤波器和高通滤波器。在本教程中，我们将学习另一类滤波器——带通滤波器。特别是，我们将学习无源带通 RC 滤波器，包括其基本电路、功能、频率响应、应用场景等更多内容。

如需了解更多关于低通或高通滤波器的信息，请阅读以下教程：无源高通 RC 滤波器、无源低通 RC 滤波器、有源高通滤波器和有源低通滤波器。

引言

可以说，带通滤波器是低通滤波器和高通滤波器的组合。顾名思义，这种滤波器仅允许特定频率范围的信号通过，而阻断所有其他频率的信号。

在音频应用中，有时需要仅通过特定范围的频率。这些频率范围并不从 0 Hz 开始，也不在非常高频率处结束，而是位于某个特定范围内，无论是宽范围还是窄范围。这些频率范围通常被称为带宽。

无源带通滤波器

通过级联无源低通滤波器和无源高通滤波器，可以实现带通滤波器。这种组合能够提供一个选择性滤波器，仅允许特定频率通过。这种新的 RC 滤波器电路能够通过窄范围或宽范围的频率。

这种频率通过范围（无论是窄范围还是宽范围）取决于无源低通滤波器和高通滤波器的级联方式。上下截止频率取决于滤波器的设计。这种带通滤波器本质上是一个频率选择性滤波器。

上图展示了带通滤波器电路。输入信号为正弦波。低通和高通组合的特性为我们提供了带通滤波器。通过将一组 RC 元件串联，另一组 RC 元件并联，电路表现为带通滤波器。

这使我们得到了一个二阶滤波器，因为电路中有两个反应元件。一个电容属于低通滤波器，另一个电容属于高通滤波器。在输入信号没有任何变化的情况下，这个带通滤波器将通过特定范围的频率。这种滤波器不会在信号中产生任何额外的噪声。

电路的截止频率可以按以下方式计算：

$f_c = \frac{1}{2\pi RC}$

通过调整高通滤波器和低通滤波器的截止频率，我们可以获得带通滤波器所需的通带宽度。

由于这种滤波器通过一个频率范围，因此它包含两个截止频率：下截止频率 $f_L$ 和上截止频率 $f_H$。因此，通过滤波器的频率范围被称为滤波器的带宽。一般来说，电路的带宽可以通过频率 $f_H$ 和 $f_L$ 来计算。

$\text{BW} = f_H - f_L$

其中， $f_H$ 是高通滤波器的截止频率， $f_L$ 是低通滤波器的截止频率。BW 是滤波器的带宽。带通滤波器将允许高于高通滤波器截止频率且低于低通滤波器截止频率的频率通过。

这表明低通滤波器的截止频率必须高于高通滤波器的截止频率。

使用 R、L 和 C 元件的带通滤波器

使用电感、电容和电阻设计的带通滤波器电路如下所示。

带通滤波器的中心频率（也称为“谐振峰值”）可以使用以下公式计算：

$f_c = \frac{1}{2\pi \sqrt{LC}}$

其中 $L$ 是电感的电感值，单位为亨利（H）。

$C$ 是电容的电容值，单位为法拉（F）。

我们也可以设计一个使用电感的带通滤波器，但我们知道，由于电容的高阻抗，使用 RC 元件的带通滤波器设计比 RL 电路更有优势。

带通滤波器的频率响应

极点频率大约等于最大增益的频率。

带通滤波器的频率响应曲线如下所示：带通滤波器的理想特性与实际特性不同，主要是因为电路的输入阻抗。

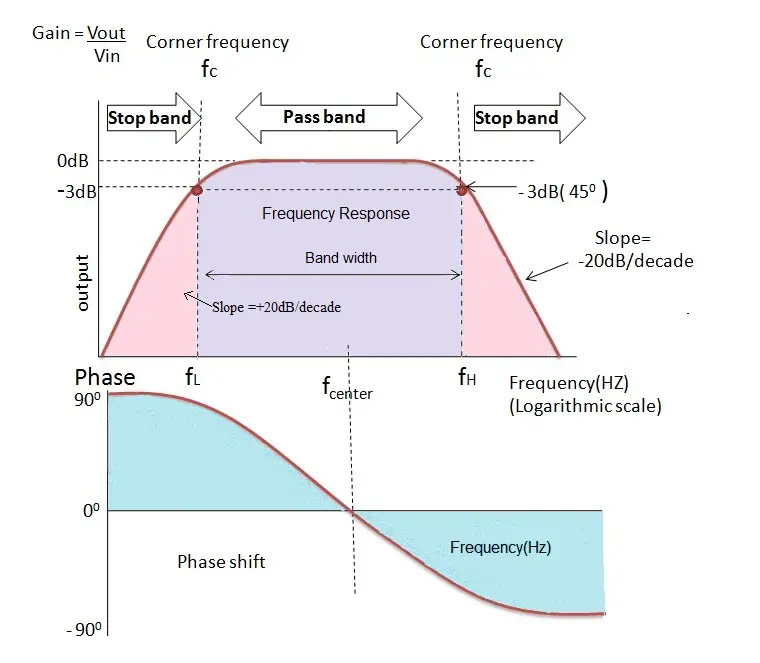
输入信号的增益可以通过计算 $20 \log (V_{\text{out}} / V_{\text{in}})$ 来得出。根据电路的固有特性，增益范围可能会相当大。信号在低频时被衰减，输出以 +20 dB/十年或 6 dB/八度的斜率增加，直到频率达到下截止频率 $f_L$。

在这个频率下，信号的增益达到 $\frac{1}{\sqrt{2}} = 70.7\%$。

在下截止频率 $f_L$ 之后，随着频率的增加，输出也会增加，增加速率为 -20 dB/十年，达到最大增益，且该增益在达到上截止频率 $f_H$ 之前保持恒定。在上截止频率之后，输出以 -20 dB/十年或 -6 dB/八度的斜率减小。

我们之前已经看到，一阶滤波器的相位偏移为 90°。我们知道，带通滤波器是二阶滤波器，因此其相位偏移是一阶滤波器的两倍，即 180°。随着频率的增加，相位角也会变化。在中心频率处，输出信号与输入信号同相。

在谐振频率以下，输出信号领先于输入信号；而在谐振频率以上，输出信号滞后于输入信号。输入信号的幅度总是大于输出信号的幅度。为了提高电路的增益，电阻 $R_1$ 的值必须大于电阻 $R_2$。

带通滤波器的中心频率

在输出增益最大的“中心频率”或“谐振频率”处，可以通过计算上下截止频率的几何平均值来得出。

$f_r^2 = f_H \times f_L$ $f_r = \sqrt{f_H \times f_L}$

其中 $f_r$ 是谐振频率或中心频率。

$f_H$ 是上 -3 dB 截止频率。

$f_L$ 是下 -3 dB 截止频率。

带通滤波器示例

假设带通滤波器允许从 1 kHz 到 30 kHz 的频率通过，并且包含一个 10 kΩ 的电阻。根据这些值，我们可以计算电容的电容值。

我们已经知道，低通滤波器的截止频率必须高于高通滤波器。因此，高通滤波器的截止频率为 1 kHz，低通滤波器的截止频率为 30 kHz。

在高通滤波器阶段：

$f_L = 1 \text{ kHz} \quad \text{和} \quad R = 10 \text{ k}\Omega$ $C = \frac{1}{2\pi f_L R} = \frac{1}{2\pi \times 1000 \times 10000} \approx 15.8 \text{ nF}$

在低通滤波器阶段：

$f_H = 30 \text{ kHz} \quad \text{和} \quad R = 10 \text{ k}\Omega$ $C = \frac{1}{2\pi f_H R} = \frac{1}{2\pi \times 30000 \times 10000} \approx 510 \text{ pF}$

从上述计算可以看出，高通滤波器所需的电容值为 15.8 nF，低通滤波器的电容值为 510 pF。

无源带通滤波器总结

带通滤波器是通过级联低通滤波器和高通滤波器实现的。由于它包含两个反应元件，因此它是二阶滤波器。滤波器的阶数取决于电路中使用的级联电路的数量。

输出信号的增益总是小于输入信号。在中心频率处，输出信号与输入信号同相；但在中心频率以下，输出信号的相位领先 +90°，而在中心频率以上，输出信号的相位滞后 -90°。

带通滤波器的实际特性与理想特性略有不同。这种差异主要是由于高通滤波器与低通滤波器的级联造成的。

输出增益总是小于1。当我们为高通滤波器和低通滤波器之间提供电气隔离时，我们可以实现更好的滤波器性能。

带通滤波器可以优化接收器的灵敏度。设计时首先加入高通滤波器，随后再加入低通滤波器。即使我们先加入低通滤波器，再加入高通滤波器，也不会对输出信号产生影响。

滤波器的品质因数取决于电阻 $R_1$ 的值。如果 $R_1$ 的值较低，则品质因数较低；如果 $R_1$ 的值较高，则品质因数较高。

带通滤波器的应用

• 带通滤波器被用于无线通信中的发射机和接收机电路。在发射机部分，这种滤波器仅允许所需的信号通过，并减少与其他电台的信号干扰。在接收机部分，它有助于防止不需要的信号进入信道。
• 带通滤波器被用于优化接收机的信噪比。
• 带通滤波器被用于光学通信领域，如激光雷达（LIDARS）。
• 带通滤波器被用于某些颜色过滤技术。
• 带通滤波器被用于医疗领域的仪器，如脑电图（EEG）。
• 在电话应用中，带通滤波器被用于DSL，以分离电话信号和宽带信号。